流匹配 和 扩散模型
这门课:Flow/Diffusion模型的理论与实践
理论:第一性原理,必要而最少量的数学知识 ODE、SDE
实践:如何实现
第零章 学习资源
https://diffusion.csail.mit.edu/
网站包括幻灯片,以及三个实验,以及课堂笔记。
第一章 利用随机微分方程的Gen AI
第一节:从生成到采样
我们将图像/视频/蛋白质表示为向量
一张图像的“好”程度 ≈ 它在数据分布下的可能性有多高
学术一点的说法:图像的质量可以近似等同于它在数据分布中的似然性
生成就是从数据分布中采样
数据分布一般用概率密度函数
数据集包含了数据分布中有限个数的样本:
条件生成指的是从条件分布中采样:
生成模型将初始分布(例如高斯分布)中的样本转换为数据分布中的样本。
第二节 流模型与扩散模型
2.1 流模型
2.1.1 基本术语和概念
流的基本对象:轨迹(Trajectory)、向量场(Vector Field)、常微分方程(ODE)
1. 轨迹:
Note
轨迹终点
2. 向量场:
Note
笛卡尔积在这里的作用是“构造一个联合空间”,就像编程里写def f(x: Vector, t: float)-> Vector:,数学中我们不能写两个参数名,所以就把它们打包成一个二元组
3. 常微分方程:描述轨迹上的条件
轨迹的导数或速度 是由
Tip
也许我们中的一些人听说过ODE在工程和物理学中是力学的基础。但“流”这个术语不太常见。流是遵循ODE的轨迹的集合。
本质上是我们收集大量针对不同初始条件的解决方案,然后将它们全部收集到一个函数中,并称之为流。
4. 流:
流
是所有不同起点 的轨迹集合,即整个系统的“流动结构”。
我们希望对于每个初始条件
所以:
ODE由向量场(VF)定义。
轨迹是ODE的解。
流则是各种初始条件的轨迹的集合。
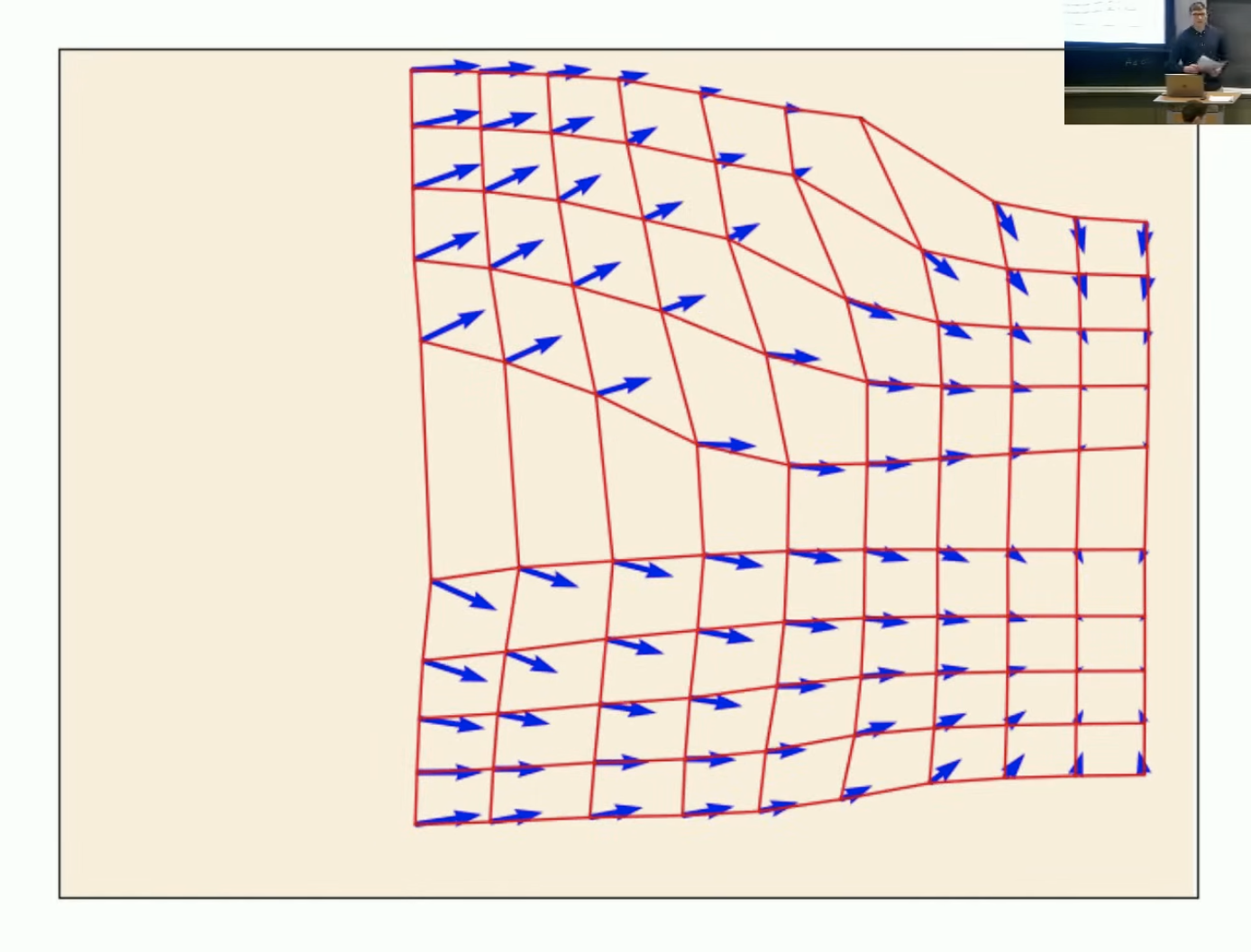
图示红色网格是轨迹,蓝色箭头是向量场。
2.1.2 定理
ODEs 解的存在性与唯一性定理
定理(皮卡–林德勒夫定理):
如果向量场
存在唯一解。换句话说,流映射是存在的。更一般地说,只要向量场是 Lipschitz 连续的,结论仍然成立。
Lipschitz 连续是一种比连续更强,比可微略弱的函数光滑性条件,在分析和微分方程中非常重要。
Tip
在机器学习实际应用中,常微分方程(ODE)或流(flow)的问题通常都存在唯一解。
你上过的大多数课程中,这已经被隐式假设了。
2.1.3 示例:线性ODE
Flow-based 模型是在学习一个确定性的(deterministic)向量场,间接决定轨迹。轨迹由向量场通过常微分方程生成。
简单的线性向量场:
断言:流由下式给出:
断言(Claim)在数学中表示一个待证明的断言、结论或命题。
发音为 /saɪ/ 或 /psaɪ/
证明:
初始条件:
ODE:
不同初始条件的轨迹:
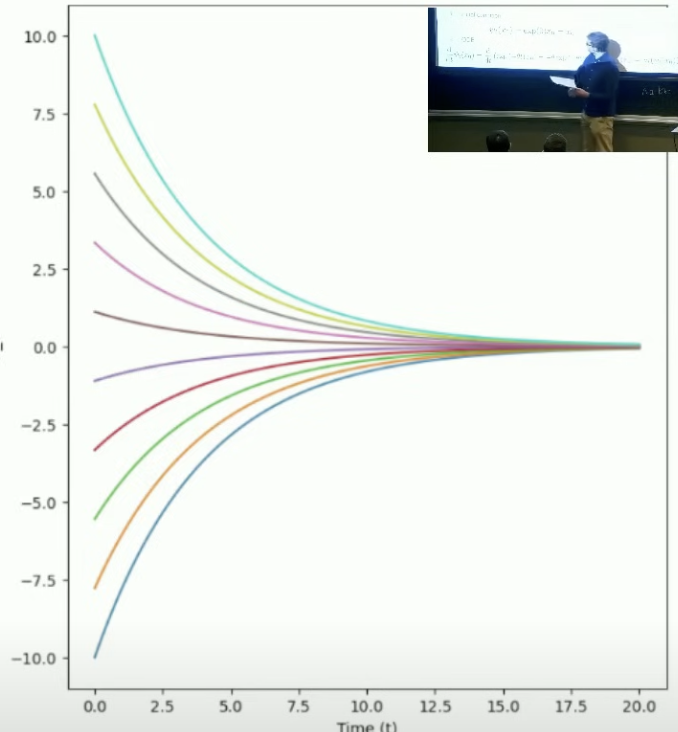
2.1.4 ODE数值模拟——欧拉法
不幸的是,在大多数情况,这并不容易,你不能只是手动找到ODE的解。
我们需要做的是模拟它。
算法1:欧拉法模拟ODE
输入:向量场
设
设步长
设
对
更新
结束循环
返回轨迹:
Tip
这是sampling的算法(生成的过程),比较简单。困难的是
2.1.5 生成模型
流模型:
神经网络:将向量场变成一个神经网络。
随机初始条件:由于ODE是确定性的,所以还不能生成整个分布。但我们可以使初始条件随机化。
常微分方程:
目标:
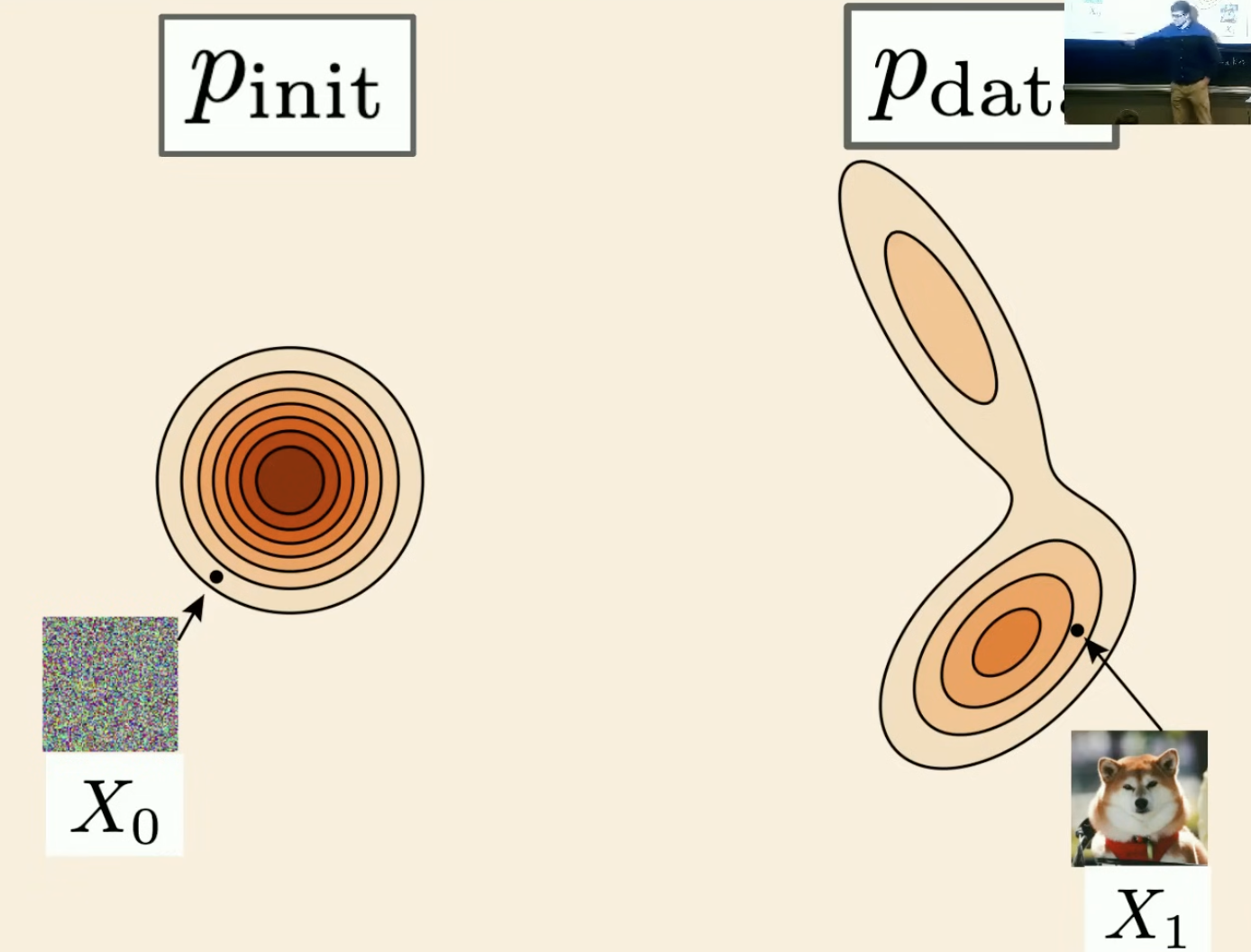
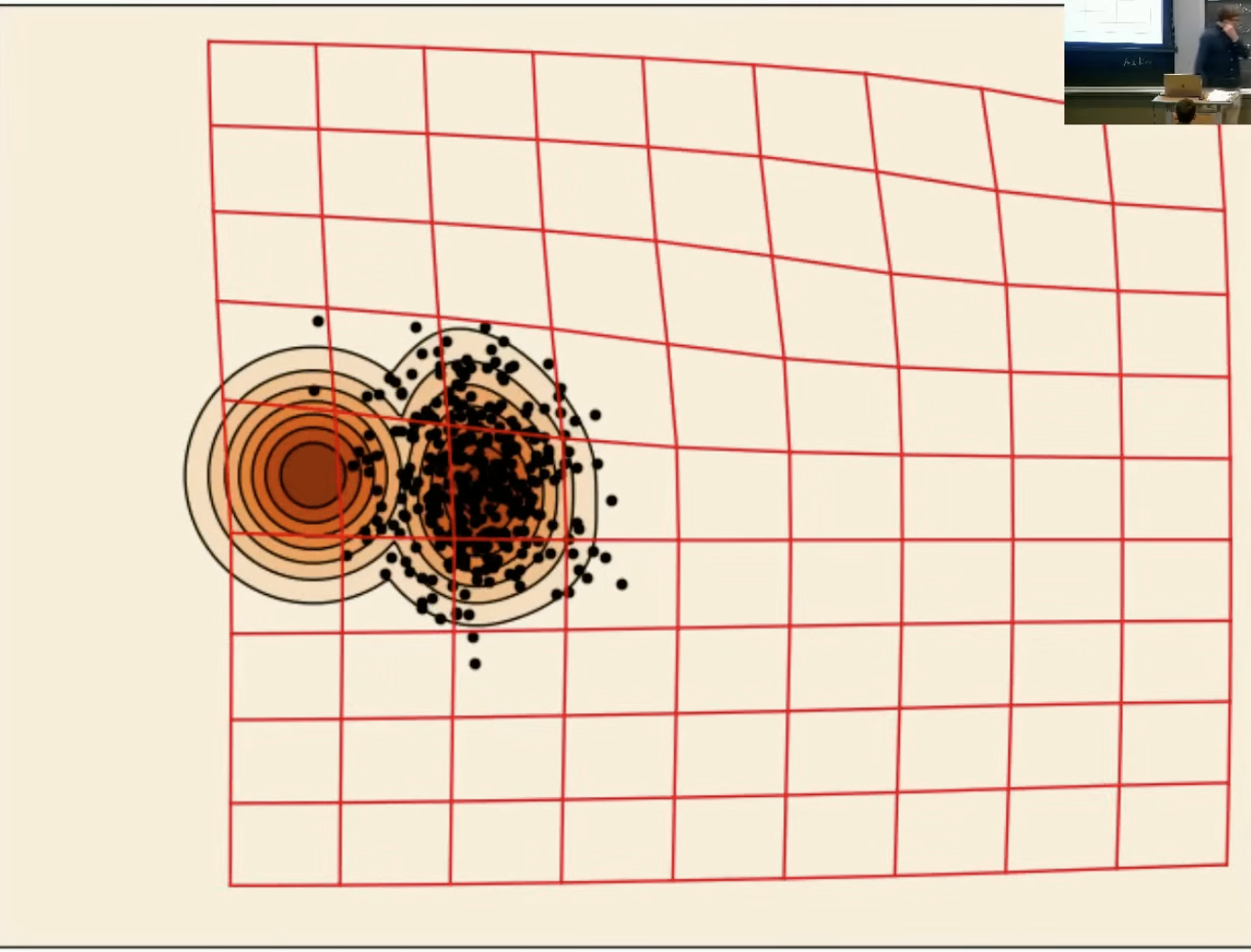
后面我们会学到,这幅图描述就是用高斯概率路径的边际向量场进行基于欧拉法的ODE数值模拟。
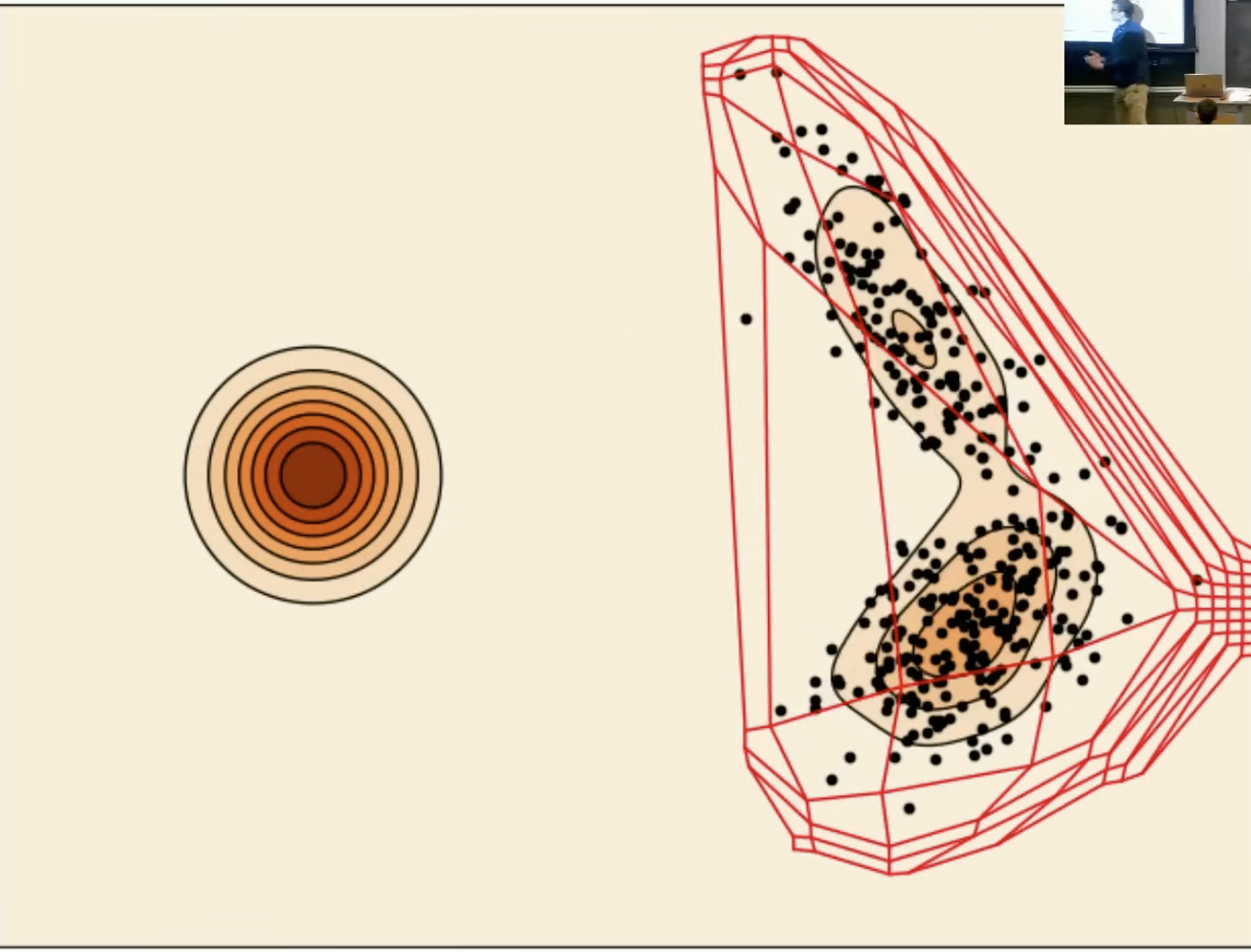
2.2 扩散模型
扩散模型本质上扩展了我们刚才讨论过的想法,但采用随机微分方程。
2.2.1 基本术语和概念
扩散模型的基本对象:随机过程(Stochastic process)、向量场(Vector Field)、常微分方程(ODE)
1. 随机过程:扩散模型的解是随机的轨迹,也称为随机过程。
2. 向量场:
3. 扩散系数:
3. 随机微分方程:
表示:
确定性部分:它会朝着一个“向量场”或“趋势”
随机部分:它还会叠加一些“不可预测的扰动”——这些扰动由布朗运动
4. 布朗运动:
随机过程:
初始化为0:
高斯增量:
独立的增量:
这个独特属性,使得它在任何地方都不可微。
但我们在研究依赖于求导的微分方程。
5. 符号
由于维纳过程不可微,我们换种表达:
这里
| ODE | SDE |
|---|---|
| 解是轨迹 | 解是随机过程,或说随机轨迹 |
| 由向量场定义。 | 由向量场 和 扩散系数 定义。 |
2.2.2 定理
SDEs 解的存在性与唯一性定理
如果向量场
存在唯一解。
2.2.3 SDE数值模拟——欧拉-丸山法
算法2:从一个SDE采样(欧拉-丸山法,Euler-Maruyama method)
输入:向量场
设
设步长
设
对
从标准
Note
更新
结束循环
返回轨迹:
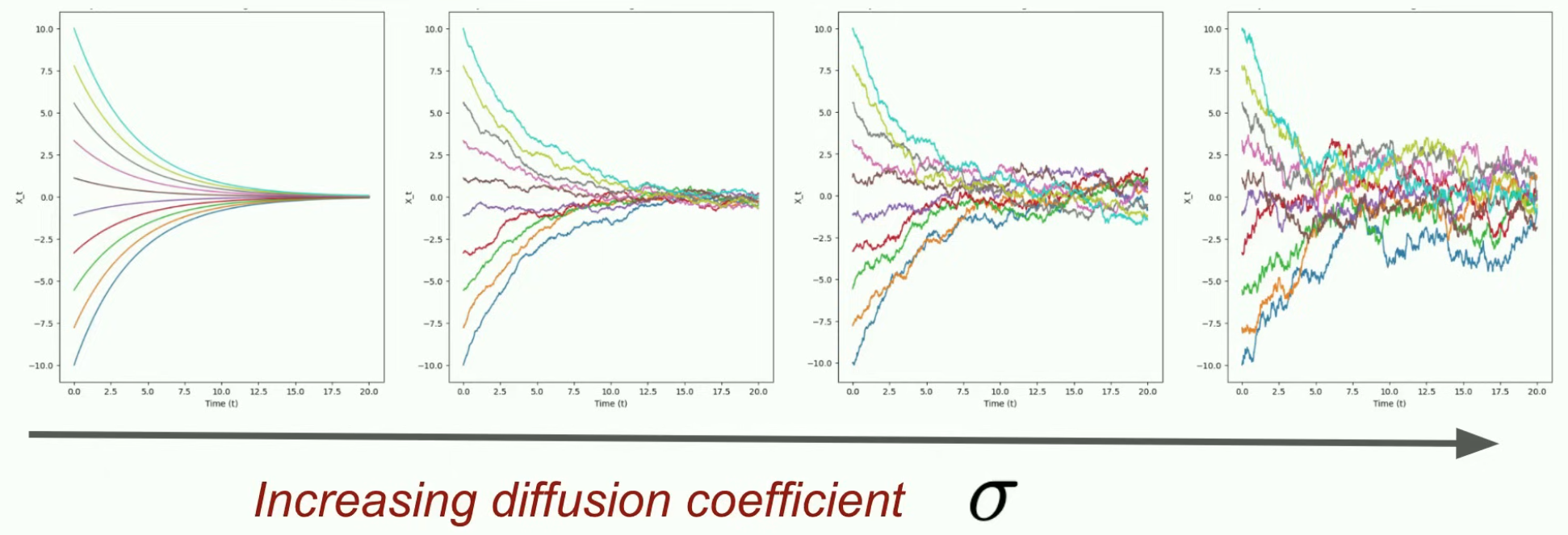
2.2.4 示例:奥-乌过程
Ornstein–Uhlenbeck (OU) 过程是一个均值回复型的随机过程,是布朗运动(随机游走)的扩展。它经常用来建模那些会在长期内回到某个平衡值附近波动的系统。
2.2.5 生成模型
扩散模型:
神经网络:是向量场,此处和流模型一样。
扩散系数:
随机初始条件:
常微分方程:
目标:
第二章 构建训练目标
回顾:
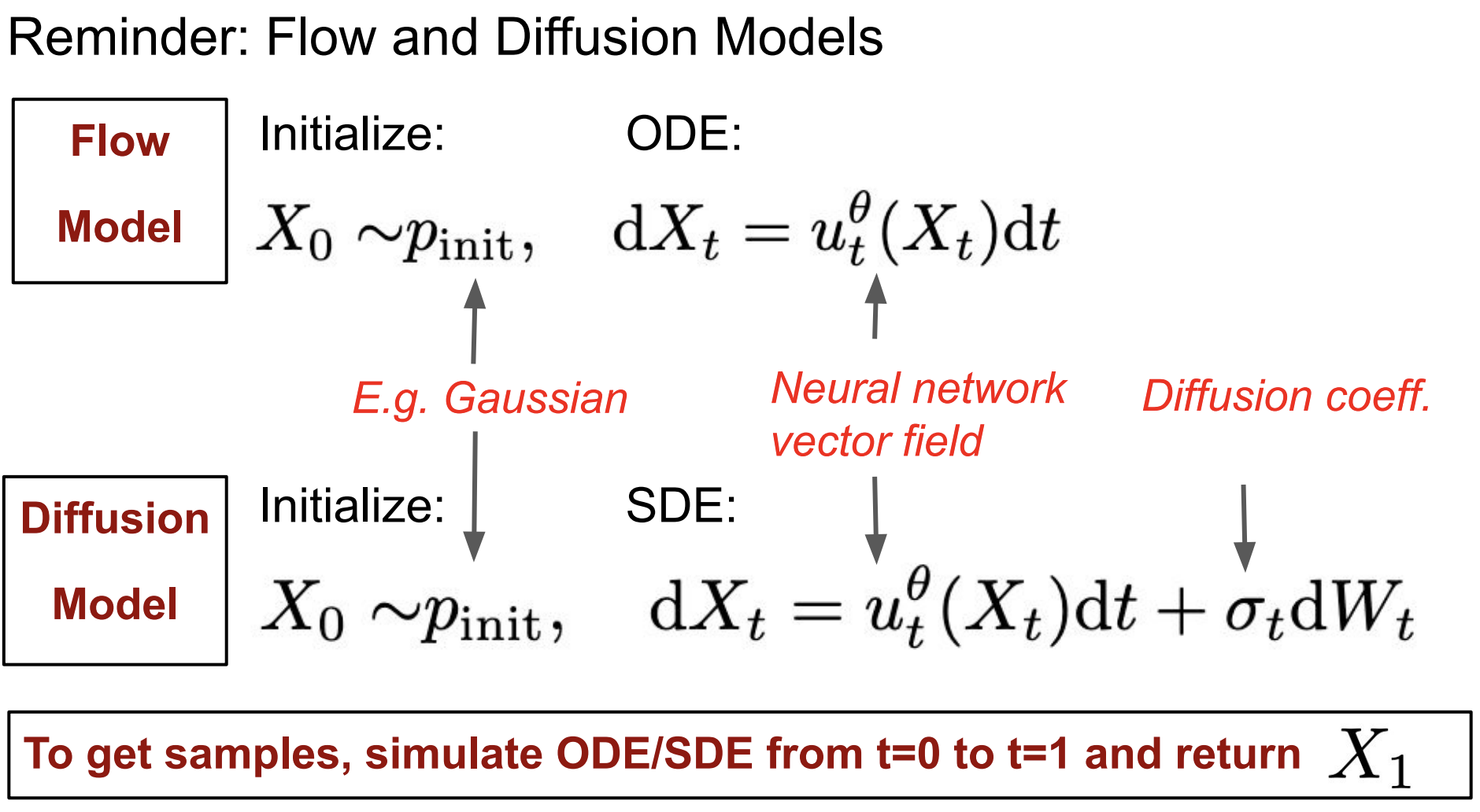
第一节 训练模型
不经过训练,模型的产出“毫无意义” → 我们需要训练向量场
训练 = 找到一组参数,使得:
在回归或分类任务中,训练目标是标签。
但在这里:没有标签 : (
我们必须推导出一个训练目标。
第二节 构建训练目标
目的:推导一个用于训练我们模型的训练目标的公式。
这一节的课程将是技术上最具挑战性的一节!接下来的课程会轻松很多很多。
你不必理解推导过程,但一定要理解以下公式:

三个条件对象,三个边际对象的公式:
条件和边际的概率路径
条件和边际的向量场
条件和边际的得分函数
2.1 条件和边际概率路径
2.1.1 关键术语
“Conditional” = “针对单个数据点”
“Marginal” = “跨数据点分布”
Conditional(条件的) 强调的是在某个特定数据点条件下的情况。
Marginal(边际的) 是指考虑整个数据的整体分布,不针对单点。
🔍 “边际”
2.1.2 概率路径
概率路径: 从噪声到数据的路径。(噪声和数据的逐步插值)
狄拉克分布( Dirac distribution):
这是最简单的一种分布。它是一种确定性分布(deterministic distribution):它在
处“无限高”,在 的地方为 0,积分为 1。 你可以把它看成一个“浓缩在一个点
上的概率分布”,所有质量都集中在 ,没有任何扩散或随机性。从 狄拉克分布中采样的结果就是 本身,毫无随机性。
Tip
一开始,大家尝试寻找“从噪声变成数据”的最优路径,比如在纯粹的神经常微分方程(neural ODEs)[1] 中,是不去指定中间过程(即路径上的中间分布)的,人们只是希望模型自己找到一条最佳路径。但扩散模型的一个关键思想,就是明确地指定从噪声到数据的演化路径。 而实际上,扩散模型这样 选择一种路径并坚持使用,是完全可行的——因为这样可以带来可扩展的训练流程。
[1] Chen, Ricky TQ, et al. "Neural ordinary differential equations." Advances in neural information processing systems 31 (2018).
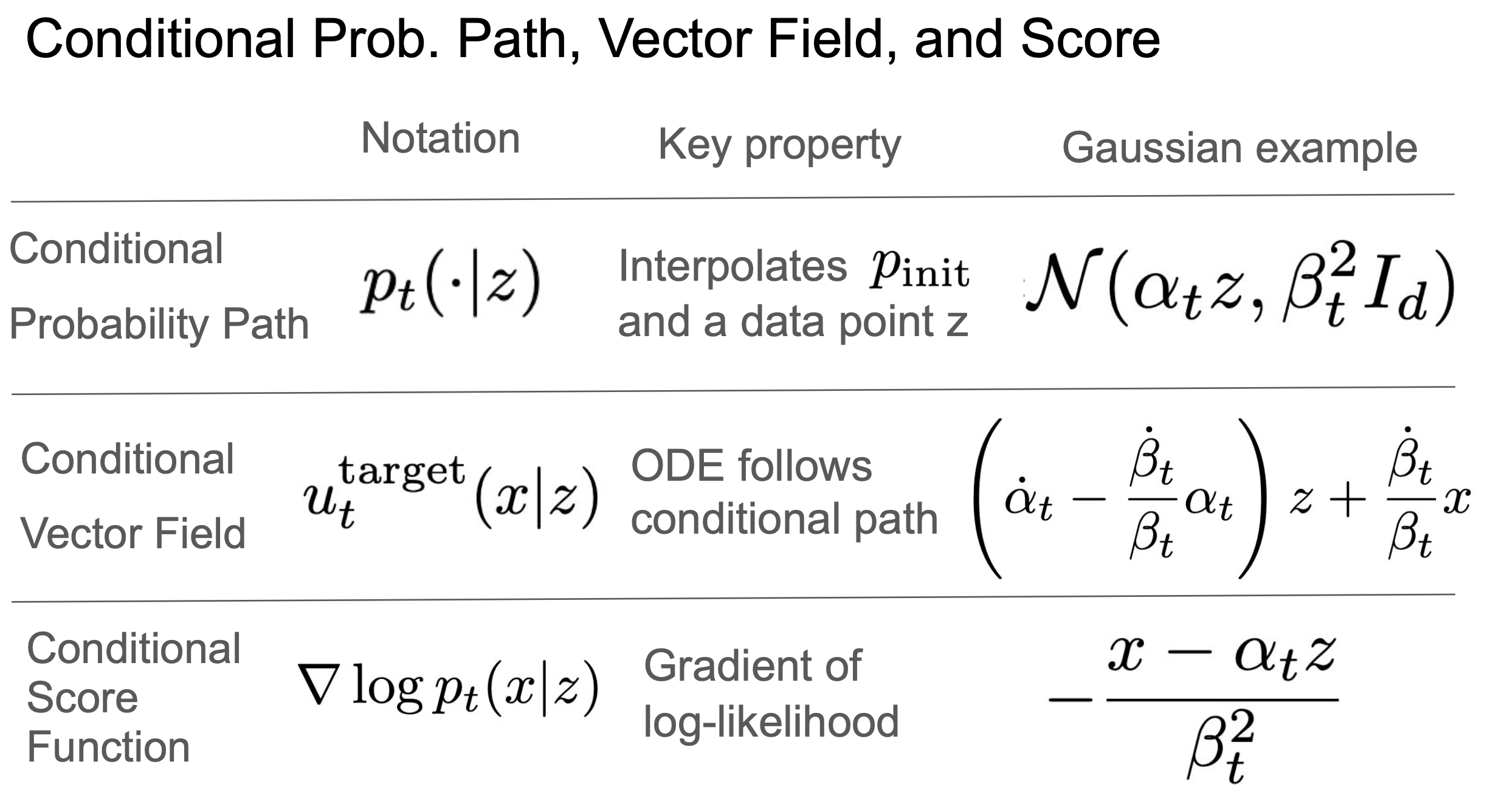
2.1.3 条件概率路径
条件概率路径:
2.1.4 例子 —— 高斯概率路径
比如常见可以设计为
容易得到,它满足条件概率路径
如下图可视化:
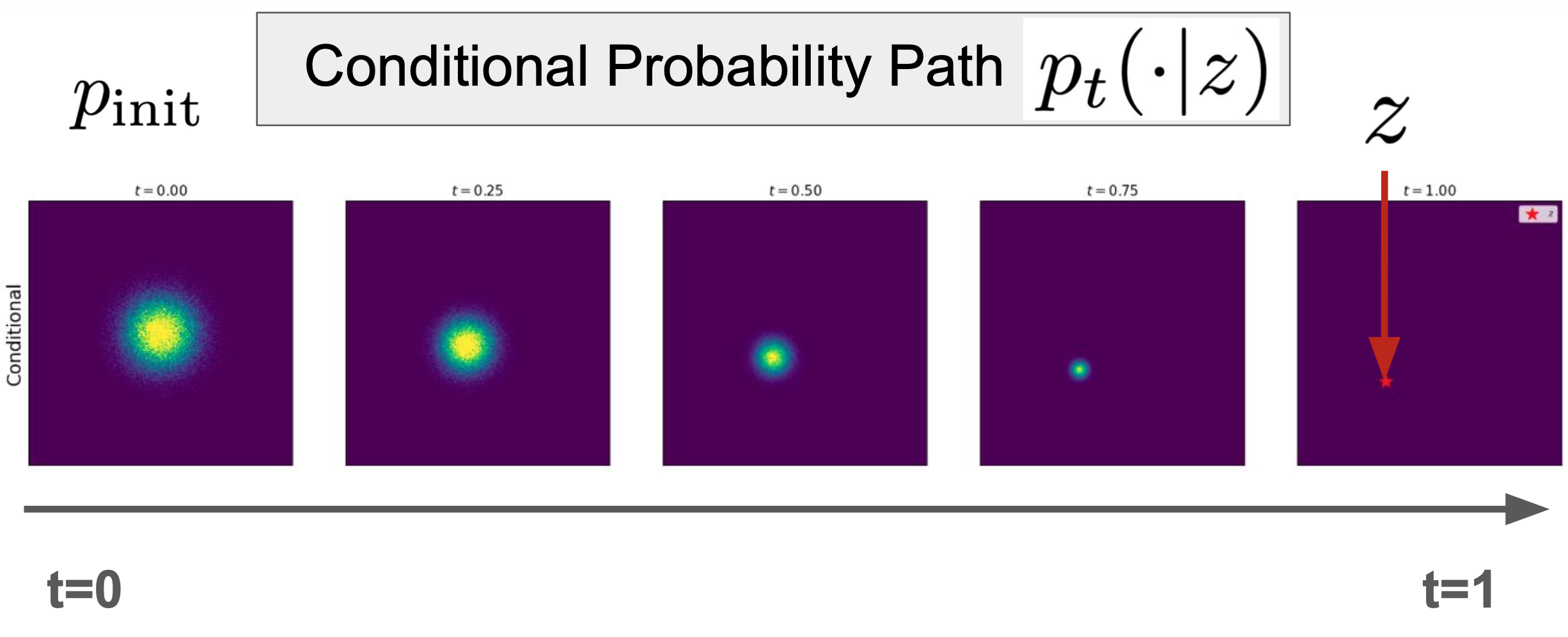
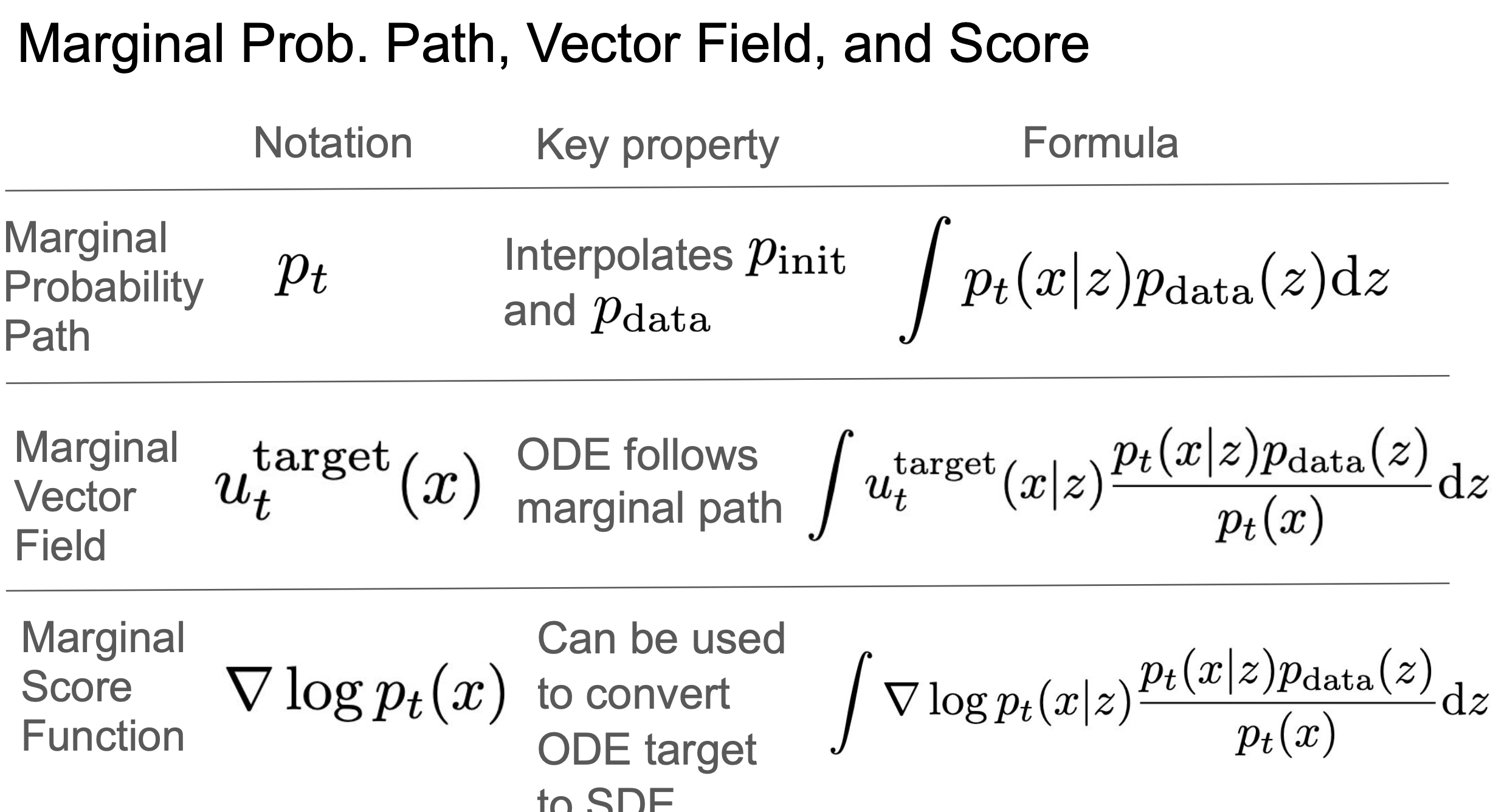
2.1.5 边际概率路径
边际概率路径:
通过条件概率路径 + 数据分布 可以推出 边际概率路径。即:
流模型中时刻
的边际分布是对所有初始数据 的条件分布 的加权平均,权重由初始数据的分布 决定。
如下图可视化:
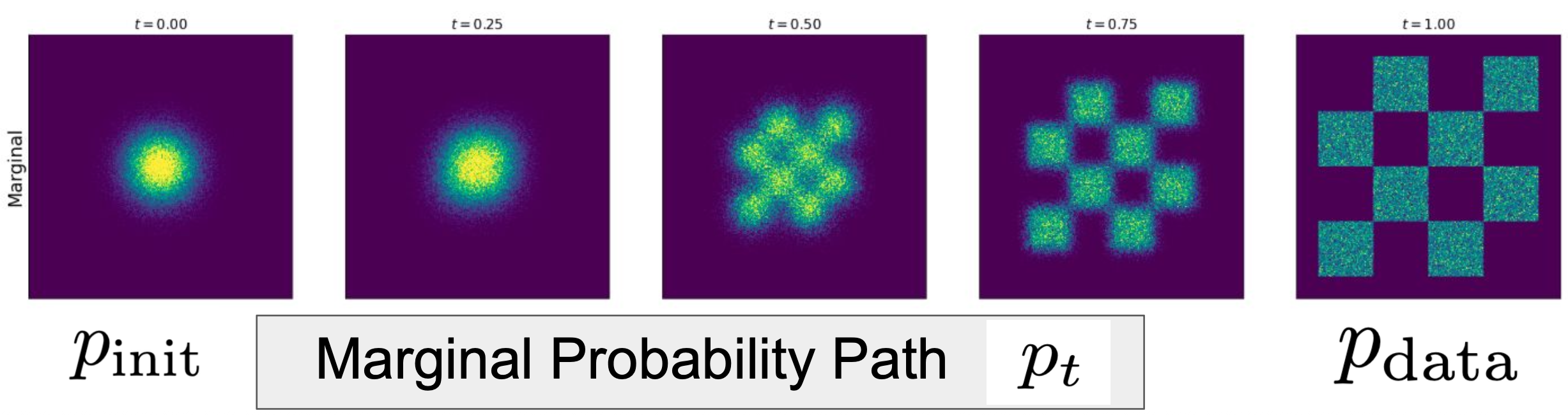
2.1.6 概率路径小结
条件概率路径
边缘化得到
边际概率路径
Note
公式
把
在概率论中,“边际”这个词来自于一个常见的操作 —— 从联合分布或条件分布中通过积分“边缘化掉”一些变量,只保留我们关心的部分。
| 术语 | 含义 | 举例 |
|---|---|---|
| 条件概率 | 给定 | 先挑定一个初始点,观察它的演化路径 |
| 联合概率 | 所有起点与终点对的联合分布 | |
| 边际概率 | 不关心 | 所有起点演化后的“总体效果” |
Tip
“边际”这个词来自表格“边缘”的历史传统,而不是因为它本身有什么边的含义。从语义角度来说确实不够直观,但它已经成为标准术语。你记住“边际 = 去掉另一个变量后,留下的总概率”就可以了。
| 性别 / 吸烟 | 吸烟 (Yes) | 不吸烟 (No) | 总计(边缘) |
|---|---|---|---|
| 男 (Male) | 30/100 = 0.30 | 20/100 = 0.20 | 0.50 |
| 女 (Female) | 10/100 = 0.10 | 40/100 = 0.40 | 0.50 |
| 总计 | 0.40 | 0.60 | 1.00 |
如果你觉得难记,大可以在心里把它当作“总分布”或“全局分布”来理解,也没问题 。
2.2 条件和边际向量场
2.2.1 条件向量场
Note
我们希望有一个ODE,能沿着条件概率路径,从噪声到单个数据点,即
形式化(公式化)表达:
满足
2.2.2 例子——条件高斯向量场
在物理中常用于表示时间导数,如速度 ,所以 这个向量场很简单,就是
和 的某种加权组合。
这个向量场能沿着高斯概率路径
可视化为下图:
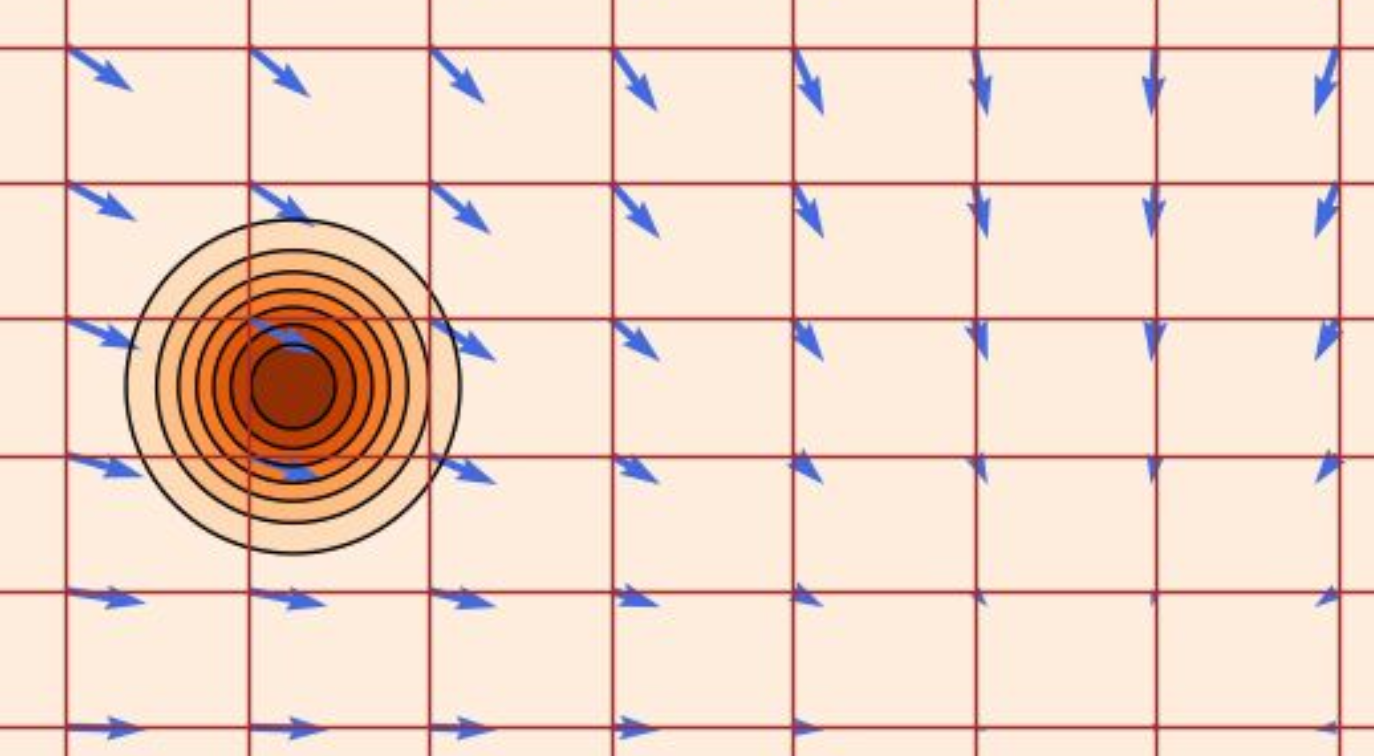
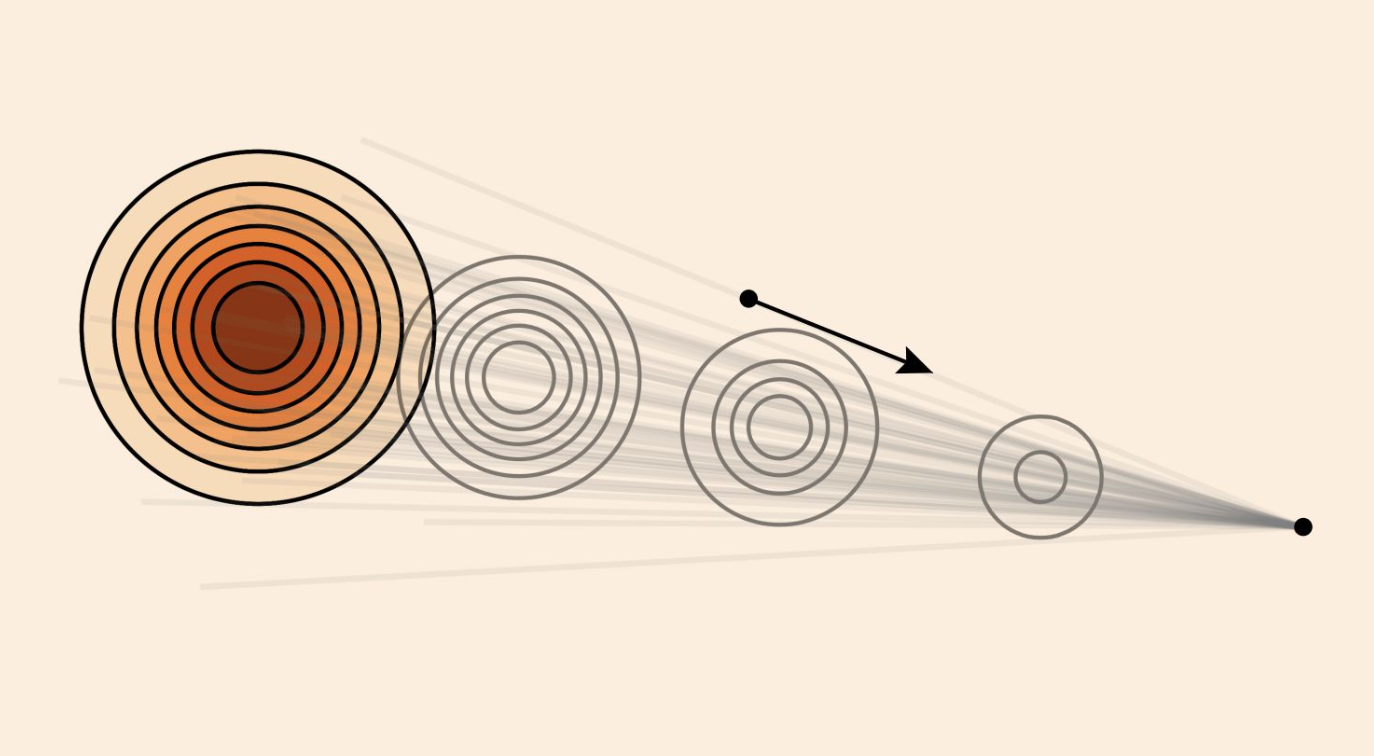
2.2.3 边际向量场 & 定理(边缘化技巧)
边际向量场:
Important
这儿要理解一下,边际概率路径是条件概率路径按
向量场描述“怎么走”的方向和速度,是动态且带方向性的。由于当前位置
这样的边际向量场
Tip
回顾这些边际对象的公式,可以看到研究 条件对象 只是工具,都是为了构建 边际对象 的公式。
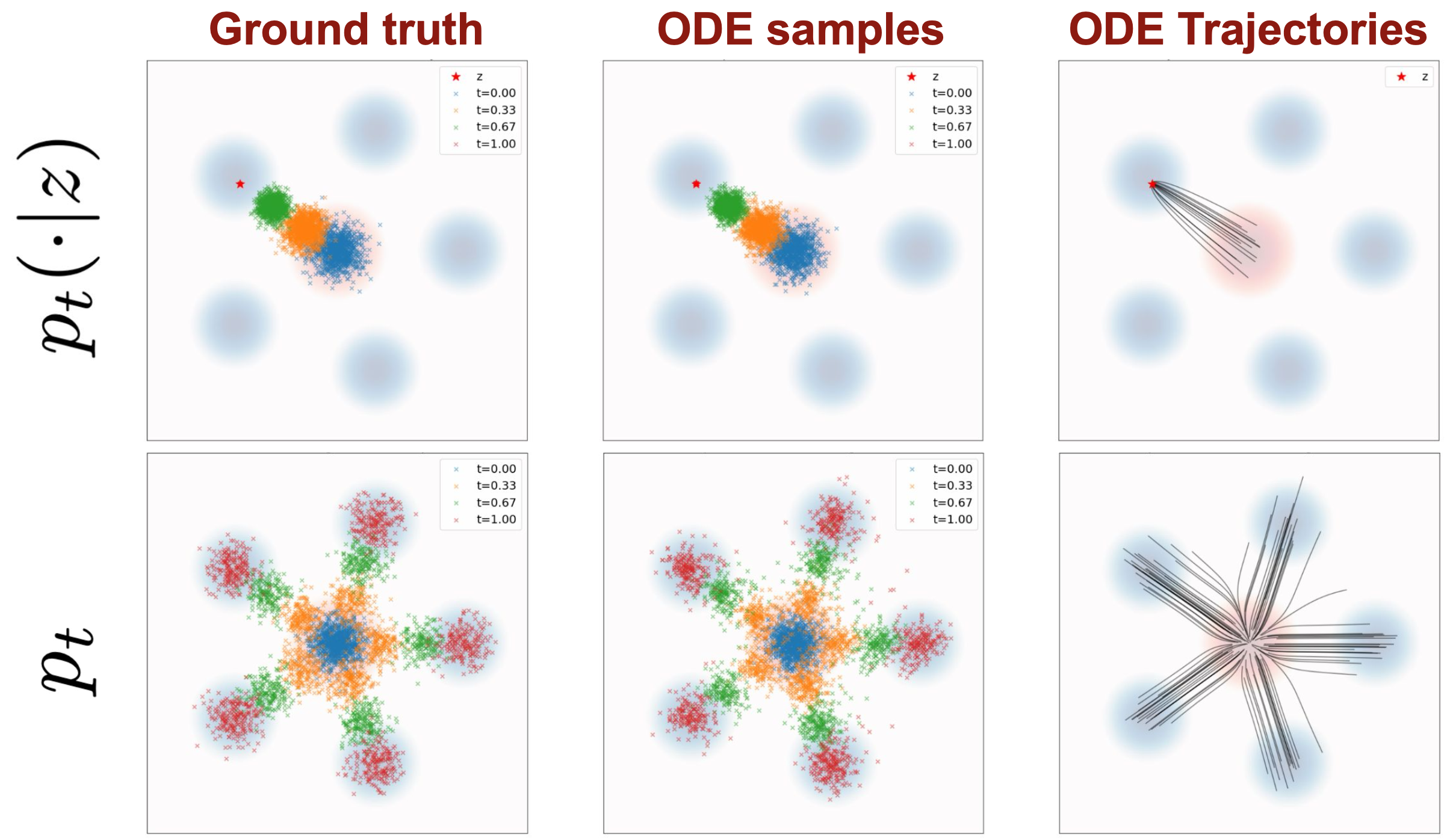
2.2.4 连续性方程(延伸知识,用于证明边际向量场的边缘化)
给定:
沿着概率路径
等价于说:
连续性方程
Note
可以理解为 概率密度的变化,取决于该点的负的净流出量。(散度衡量的是净流出量 。用于描述 流体是否在某处发散或聚集,正散度表示发散,负散度表示汇聚。)。
换句话说, 流出越多,密度下降越快。
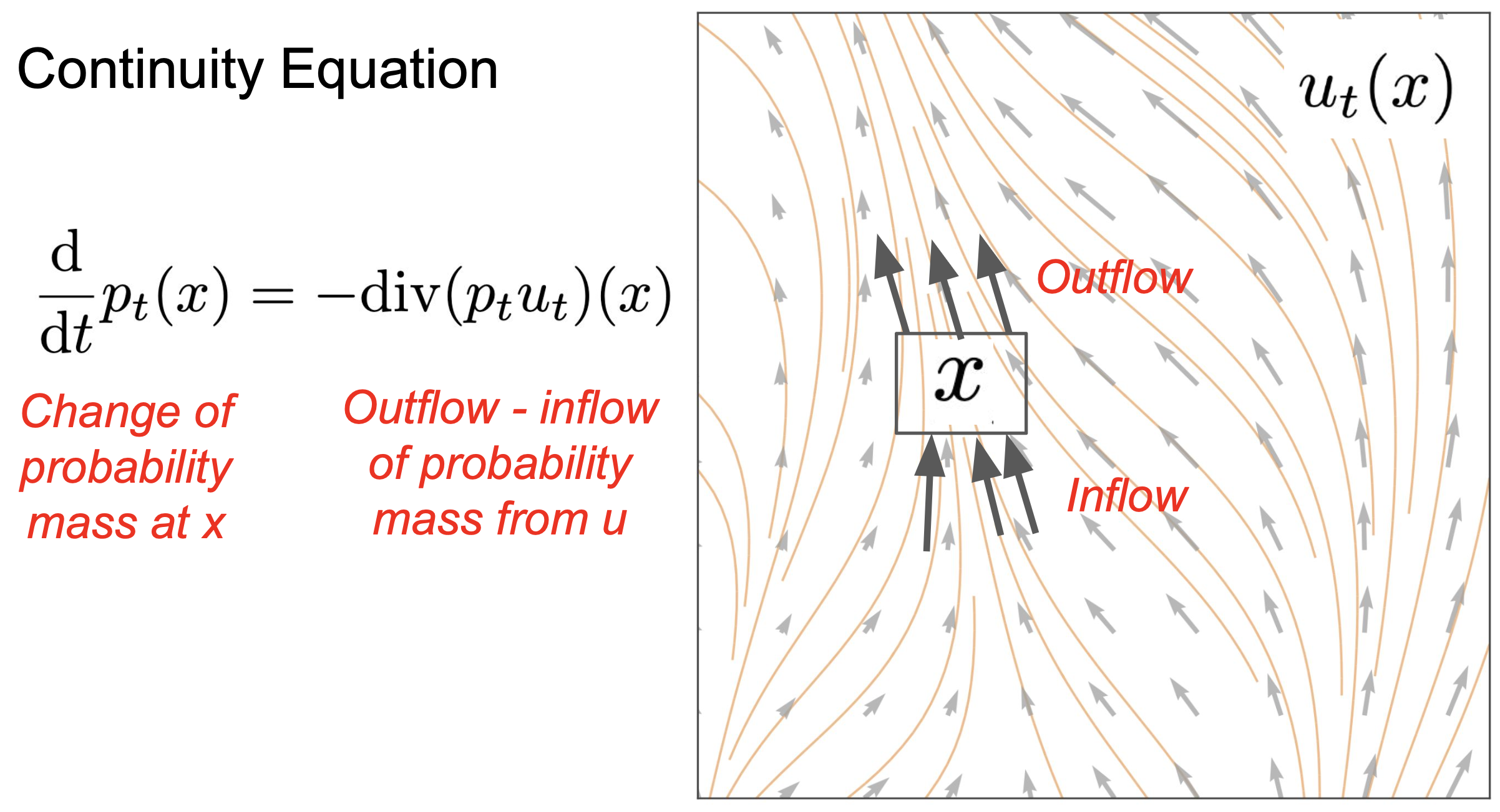
Caution
向量场的散度是描述流体“是否在某处发散或聚集”;
散度:
而KL散度是描述两个分布“偏离有多大”。从数学形式和语义来看,它们是两个完全不同的工具。
仅仅因为字面的 “偏离/发散” 符合描述,而使用了相同的术语词汇。
证明:
Tip
其实就是利用连续方程:
的定义
,在推导过程中,得到的
2.2.5 向量场小结
条件向量场
边缘化得到
边际向量场
2.3 条件和边际得分函数(扩散模型)
2.3.1 条件和边际得分
条件得分:
边际得分:
公式:根据链式法则
2.3.2 例子——高斯得分
一个高斯概率路径对应的高斯得分:
由正太分布的概率密度函数
代入
推导得到。
2.3.3 定理(SDE扩展的技巧)
对于任意
Note
得分函数 本质上就是 我们需要应用的校正项。
得分函数校正了“随机扩散轨迹”的方向,让它向数据靠近。
🔍 流模型 其实就能达到这个目标,所以现在50%的模型都纯流模型。所以我们优先掌握流模型,扩散模型只是其扩展。
流模型是基础。 扩散模型更多像一种实践经验,在流模型基础上,通过实验发现加各种扩散系数的噪声,生成效果是否会改善。
2.4 总结
后续课程会学习到:
模型训练 就是 训练

第三章 训练流模型和扩散模型
回顾:



Note
知识小灶:
归一化流:直接学映射函数
像修一条高速公路。你得明确规划每个路口(映射函数),并且每段必须符合标准设计(可逆、结构简单、Jacobian 可计算)。
流匹配:学导数(vector field) 像使用GPS。你不关心路具体长什么样,只要告诉我每个时刻往哪个方向走(向量场),然后用 ODE 把路径积分出来,就能从出发点走到终点。
3.1 训练算法
我们将 边际向量场、边际得分函数 转化为 两种算法:流匹配 与 得分匹配。
这将是训练算法,用于学习这两个对象。

3.2 流匹配
目标
3.2.1 流匹配损失
✓ Minimizer ✗ Tractable
为什么不易处理呢? 因为我们无法评估这一点,边际向量场是一个(边缘化)积分,批量进行计算很困难。
Note
这里流匹配损失函数很直观,就是两个对象之间的均方误差。取期望值就是在所有采样样本torch.mean,这是平时实现损失函数常用的。
3.2.2 条件流匹配损失
? Minimizer ✓ Tractable
最小化这个对象是否有意义?因为条件向量场不是真的有用,我们不想生成单个数据点,而是想生成整个数据分布。
但接下来我们会证明,最小化条件流匹配损失,能够达到我们的目标。
3.2.3 定理
Tip

3.2.4 算法(通用)
算法3:流匹配训练过程(通用)
输入:一个样本
对每个最小批次(mini-batch)的数据循环:
采样
采样
采样
计算损失
(选择一种优化器)梯度下降更新模型参数
循环结束
Note
流和扩散模型的强大之处就在于只需要最小化简单的均方误差。例如,GANs会有一个最小最大优化程序,比这复杂得多。
这儿条件概率路径
3.2.5 例子——高斯概率路径的
回顾:
继续推:
, , 代入
再做些代数:
对于指定的条件路径的实例:
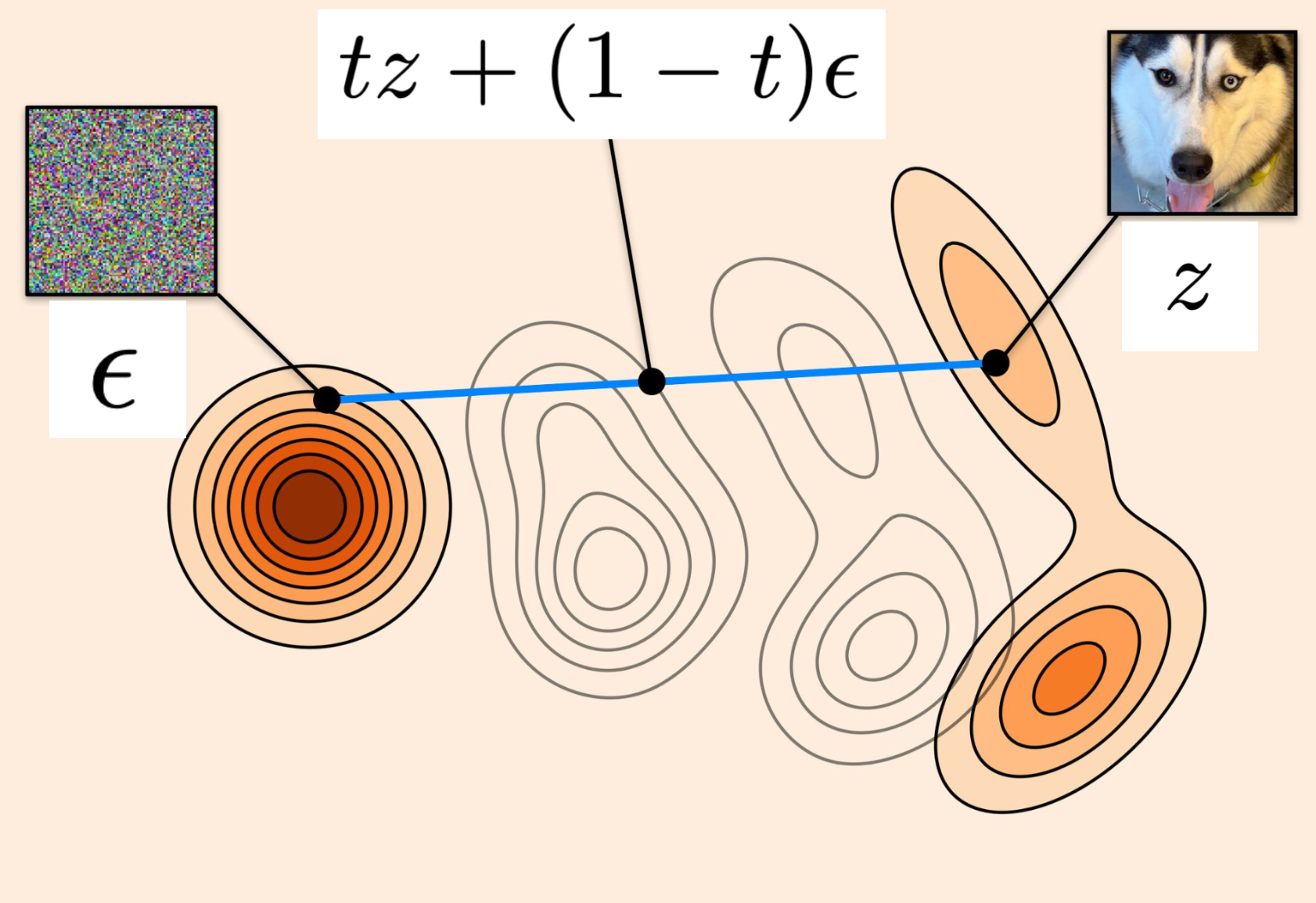
Tip
Cond OT path
选择的
有:
非常简单吧,无法想象一个更简单的训练算法了。
3.2.6 算法(OT)
Flow Matching Training for CondOT path
算法4:流匹配训练过程(最优传输路径)
输入:一个样本
对每个最小批次(mini-batch)的数据循环:
采样
采样
采样噪声
设
计算损失
(选择一种优化器)梯度下降更新模型参数
循环结束
Important
让我们欣赏下该算法的简单:
我们在
Tip
思考:为了训练更稳定,采样
物理直觉:
本质上是在预测给定噪声、数据点和路径,在这条路径上的某个地方,你需要预测当前的速度。但在直线路径(OT)中,速度只是一个差值,两点间的向量。
而扩散模型走的是非直线,就像一些所谓的方差保持路径或方差爆炸路径。
这可不是什么奇特的、太简单的算法,MovieGen(Meta)、Stable Diffusion 3(Stability AI)就是用的该算法。
3.2.7 证明
对定理:
然后
和 是和 无关的常数,可以消掉, 项相同,也可以消掉。
转变成了证明
3.2.8 采样算法
我们如何从刚刚训练好的流模型中采样(生成对象)呢?
参加算法1 ODE数值模拟——欧拉法
Tip
问:人们是否使用欧拉法?
答:最初是的,但现在人们最想要最小化神经网络的预测次数,也就是数值模拟中有多少步。所以关心效率时,人们通常使用高阶ODE求解器。
Euler 方法(欧拉法)是最基本的 ODE 数值求解器之一,属于一阶(first-order)ODE solver。
“higher-order” 指的是方法的收敛阶(order of accuracy),也就是它逼近真实解的速度。
3.3 得分匹配
回顾:
边际得分函数:
定理(SDE扩展的技巧):
对于任意
Note
得分函数 本质上就是 我们需要应用的校正项。
得分函数校正了“随机扩散轨迹”的方向,让它向数据靠近。
3.3.1 得分匹配损失
得分匹配网络:
目标:
由于边际得分函数和边际向量场的(边缘化)公式非常类似,这儿的推导也是类似的,即将证明:
Note
人们习惯将条件得分匹配损失,称作去噪得分匹配损失。实则是一回事。
3.3.2 去噪得分匹配损失
✓ Minimizer ✗ Tractable
? Minimizer ✓ Tractable
3.3.3 定理
3.3.4 算法(通用)
算法5:得分匹配训练过程(通用)
输入:一个样本
对每个最小批次(mini-batch)的数据循环:
采样
采样
采样
计算损失
(选择一种优化器)梯度下降更新模型参数
循环结束
3.3.5 例子——高斯概率路径的
回顾:
继续推:
Tip
现在你应该理解,为什么它被称为 去噪得分匹配,是因为被发现对于高斯概率路径,我们只是学习预测用于破坏数据点的噪声。
3.3.6 算法(高斯概率路径)
Score Matching Training for Gaussian probability path
算法6:得分匹配训练过程(高斯概率路径)
输入:一个样本
输入:Schedulers
对每个最小批次(mini-batch)的数据循环:
采样
采样
采样噪声
设
计算损失
(选择一种优化器)梯度下降更新模型参数
循环结束
Note
值得一提的是,对于较小的
扩散模型研发的早期就意识到这点,并且有一些技巧可以解决。在课堂笔记里有介绍。 但得分匹配是在扩散模型之前就提出的,那时人们反对这种匹配具有高方差。
问答:
Note
问:我们能否避免同时学习它们(流匹配网络 和 得分匹配网络)?
答:其实我稍后会讲到这个。答案是肯定的。
原则上,对于一般情况,你必须同时学习它们。
但是,在最重要的特定的高斯概率路径,我们可以将它们相互转换。
但即使你必须同时学习它们,请记住,我们可以将它们放在同一个网络中,也就是为一个图像的每个像素制作两个输出,所以它的计算成本不会那么高。
3.3.7 采样算法
扩散模型的随机采样:
我们将训练好的新网络插入到SDE:
经过训练
3.3.8 去噪扩散模型(DDMs)
术语
去噪扩散模型 = 高斯概率路径
通用术语中 Terminology(by many people)
去噪扩散模型 = 扩散模型
也就是说,许多人提到扩散模型,就是指的这个特定的实例。人们会用不同的方式谈论同一件事。
当和你的同事交谈时,他们会用一种完全不同的语言,不要感到困惑。这并不奇怪,因为算法是通过许多不同的方式发现的。
特殊性质
向量场和得分函数 可以 相互转换。 所以同一个网络即可完成 流匹配 和 得分匹配。
经过代数,就能得出它们能相互转换:

训练后的边际向量场 可以转换为 得分网络,反之亦然。
即,得分是免费获取的。
Tip
所以第一代的扩散模型文章,只讨论 得分匹配。 因为它们隐式地依赖于高斯概率路径的去噪扩散模型。然后可以将东西相互转换。
总结
我们在这里得到一个完整的端到端训练和采样算法。我们有一个通用的模型,可以从数据分布中生成样本。
下周的课程将更加注重应用,我们将讨论针对特定应用可以做出的具体选择:
神经网络架构,即
基于提示词的条件
图像生成器 或 视频生成器
其他应用:机器人技术、蛋白质设计
我们可以将任意分布相互转换,任意的
但可能还有其他情况,你的初始分布要有趣得多,而且有很多人在探索这一点。
在图像空间、音频空间以及科学领域,许多时候,你的初始分布本身就很有意义,例如:

我觉得可以预测转换域的东西,定义清楚这个转换,是光流?是高频残差?等等。 有意义的输入则作为参考信息。
第四章 构建一个图像生成器
为了避免混乱,本章只以流模型为例,进行介绍。但所讲述的内容都可扩展到扩散模型。
议程:
将生成模型框架从 无条件生成 延伸到 有条件生成。
开发用于条件采样的无分类器引导(classifier-free guidance)方法。
讨论图像生成这一典型案例中的架构选择,并综述当前主流模型。
4.1 条件生成和引导
无条件 也可以 称作 无引导(Unguided)
有条件 也可以 称作 有引导(Guided)

4.1.1 有引导的条件匹配目标函数
观察:当
此时
可以理解为 超参数。
观察:当让
4.1.2 无分类器引导(CFG)
| 名称 | 定义 | 是否使用条件? | 是否用分类器? |
|---|---|---|---|
| 无引导生成 (unconditional generation) | 不提供任何条件,模型自由生成样本 | ❌ 否 | ❌ 否 |
| 有引导生成 (conditional generation) | 提供条件(如文本、类别)来控制生成 | ✅ 是 | ✅ / ❌ |
| 有分类器引导 (classifier guidance) | 使用独立的分类器来引导生成趋向目标类别 | ✅ 是 | ✅ 是 |
| 无分类器引导 (classifier-free guidance) | 不使用分类器,而是训练一个能同时进行有/无条件生成的模型,在推理时人为混合 | ✅ 是 | ❌ 否 |
无引导生成:用于评估模型的基础能力;或生成多样化样本;
有引导生成:
有分类器引导:早期的方法,但需要训练或提供外部分类器;
用另一个分类器告诉模型“图像像不像
本质:用分类器给的方向来指导生成
实现:要给图像打分,然后反向传播出“变得更像 y”的梯度
缺点:慢,要用梯度反传,还要额外训练一个分类器
无分类器引导:现代主流方法,易实现且效果好。
用模型自己预测“有条件”和“没条件”两种方向,然后人为混合,走向更像 y 的方向。
本质:用模型自己两个版本的预测结果做“加权”
实现:直接:
优点:快!只用一个模型,不用分类器也不用反传梯度
Tip
问:为什么不能对有分类器引导也这么加权?
答:因为它的“引导方向”是用分类器反传出来的梯度(方向),不是一个完整的预测向量场,你没法跟另一个向量直接相加。 而 classifier-free guidance 是两个完整的模型输出,当然可以直接加。
无分类器引导(Classifier-Free Guidance) 是一种 启发式方法,通过线性组合模型在有条件与无条件下的预测结果,来构造一个引导向量场,以实现条件控制。
有分类器引导(Classifier Guidance) 是一种 理论驱动的方法,直接利用一个额外分类器
相当于对于
有分类器引导的
4.1.3 CFG推导
对两边求导有:
其中
实际操作中,直接用上式做采样,往往会弱化条件的引导效果,所以提出了引入一个超参数
因为
与 无关,对 的梯度是0。
Note
符号
推出 无分类器引导(classifier-free guidance)的 核心思想在向量场形式上的表达。
我们用有条件和无条件的向量场按比例加权,得到一个“折中”方向,来引导采样过程。
4.1.4 CFG训练
观察:我们可以将无引导的向量场视为没有任何条件的情况。 但“没有条件”也是一种条件:
我们现在可以训练一个单一模型
4.1.5 CFG采样
每一步都调用模型两次(无条件 & 有条件),计算量是原来的两倍。但是工程上有些优化方法。
算法——CFG采样过程
输入:训练好的有引导的向量场
选择一个提示词
选择一个引导尺度
初始化
从


4.2 图像生成的网络架构考量
对于图像这种高维的对象,多层感知机(MLP)是不够的。
我们将探索两种选择:U-Nets(基于卷积)和 DiT(基于注意力)
留意 引导变量